by

Laws of Motion

Force

  • The concept of force gives us a quantitative description of the interaction between two bodies or between a body and its environment.
  • A force is a push or a pull.
  • It is a physical quantity that has both magnitude and direction.
  • For example if a string is attached to one edge of a book and the string is pulled vertically. the book tilts about its opposite edge. But if the string is attached to the middle of the book and pulled vertically, no tilting takes place.
  • The following factors determine the effect that a force has no a body :
  1. The magnitude of force applied
  2. The direction in which force is applied
  3. The point of application of force.

KINDS OF FORCES

Field force (F)

Forces which act between the bodies when bodies are not in contact are called Field forces.

For this the body has to be present within a specific region of space around the other body. This region of space is called the ‘field’ of the other body.

For example gravitational force, electromagnetic force etc. are known as field forces.

Gravitational Force or Weight of the body:

The force with which earth attracts a body towards its center, is called gravitational force on it or the weight of the body.

When the body is close to the surface of earth, the weight of the body acts at its center of gravity and its direction is vertically downward.

Contact force (F)

Forces which act when bodies are in contact are known as contact forces.

[It is usually convenient to resolve contact forces into components, one parallel to the surface of contact, the other perpendicular to the surface of contact.]

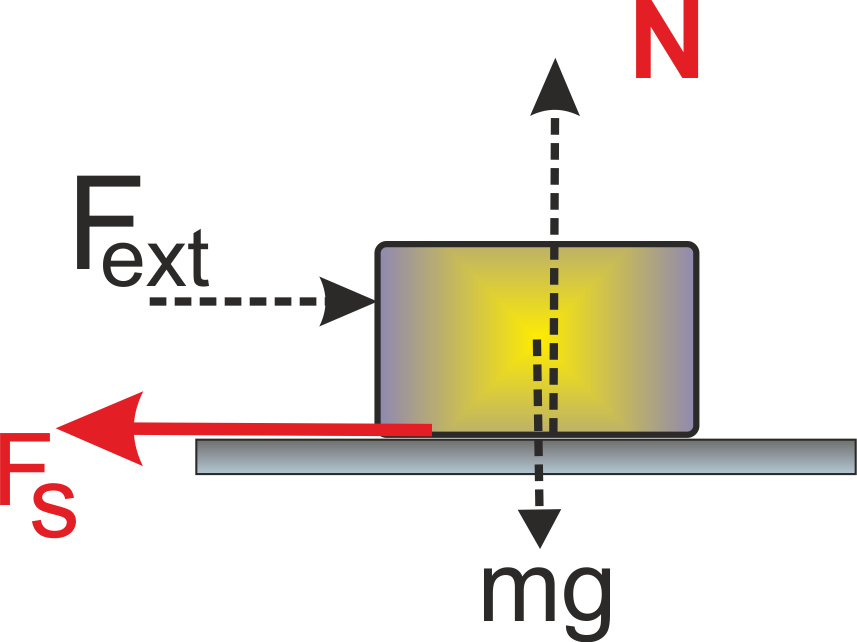
Normal force or Normal Reaction (N) :

The component of the contact force that is perpendicular to the surface of contact is known as the Normal reaction force. It measures how strongly the surfaces in contact are pressed together.

Normal force is a self-adjusting force and its value depends upon other forces acting on the body.

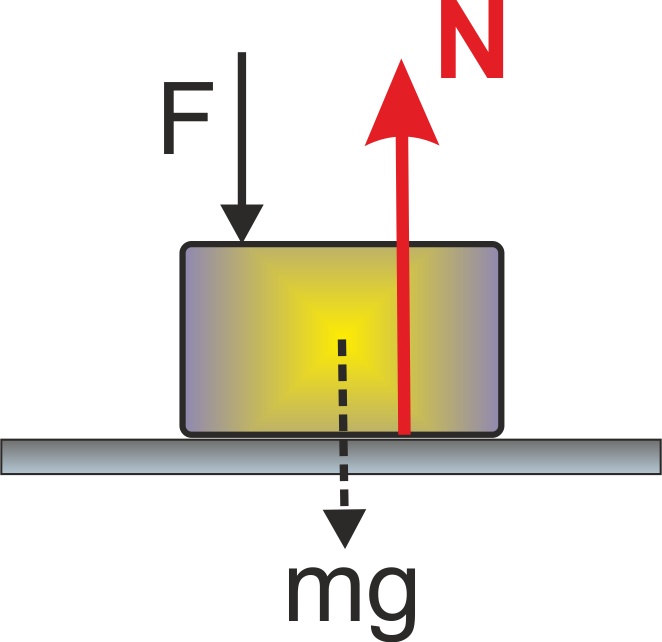
normal force on horizontal support
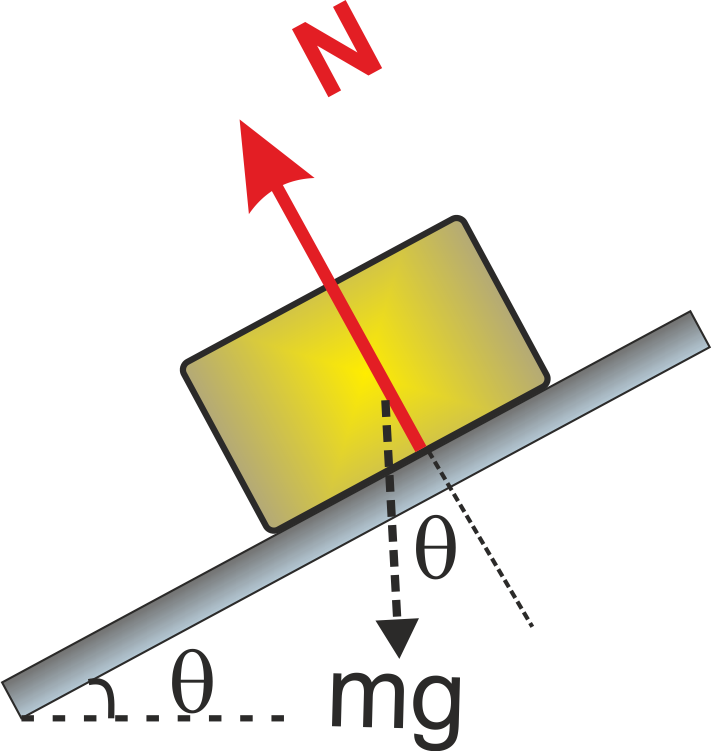
Normal force on inclined support
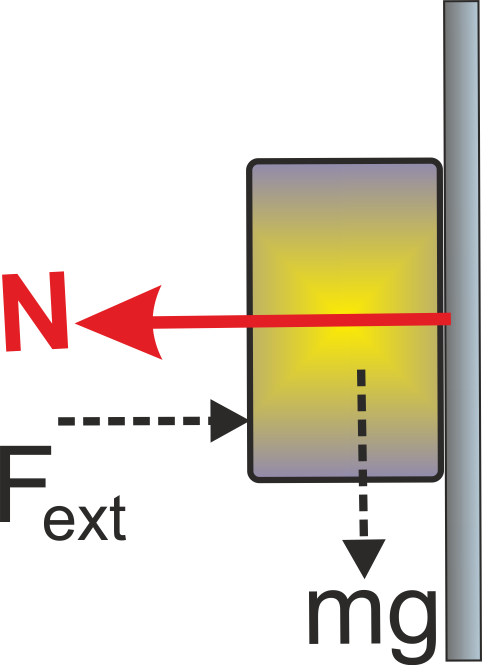
Normal force by vertical support
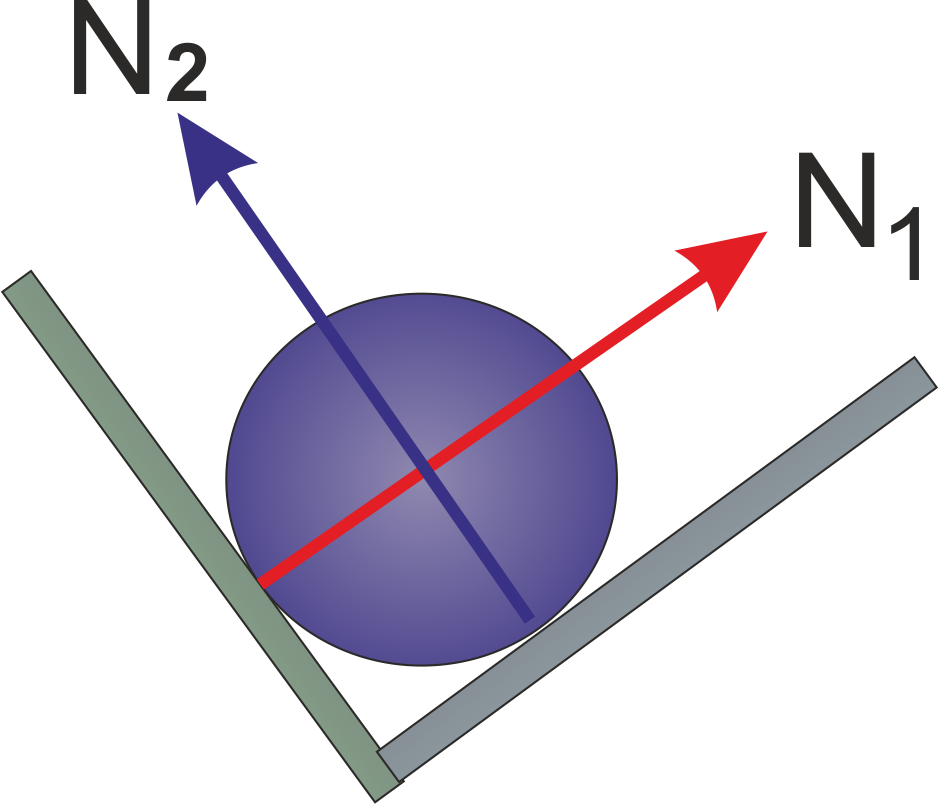
Normal force by two supports

Examples of Normal Forces in different situation.

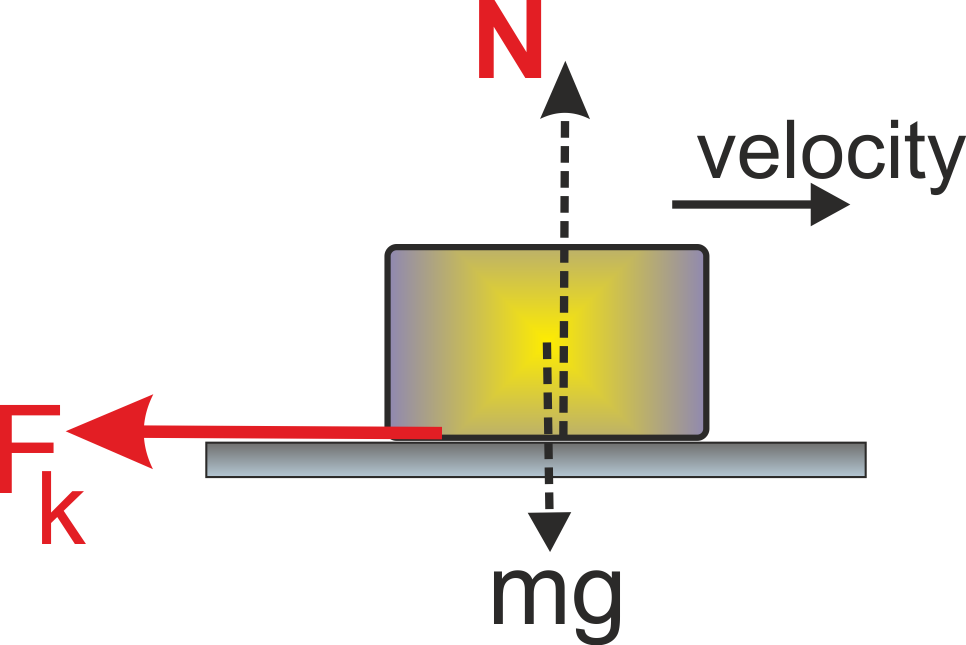
Frictional Force (f) :

It is the component of the contact force parallel to the contact. The direction of the force of friction is opposite to the direction of relative motion between the surface, or is such as to oppose any tendency of relative motion between the surfaces.

Tension: (T)

When a body is connected by means of string or a rope, a force may be exerted on the body by the string or the rope. This force is called tension.

  • If a string is ideal (inextensible and massless), then the magnitude of the acceleration of any number of masses connected through this string is always same.
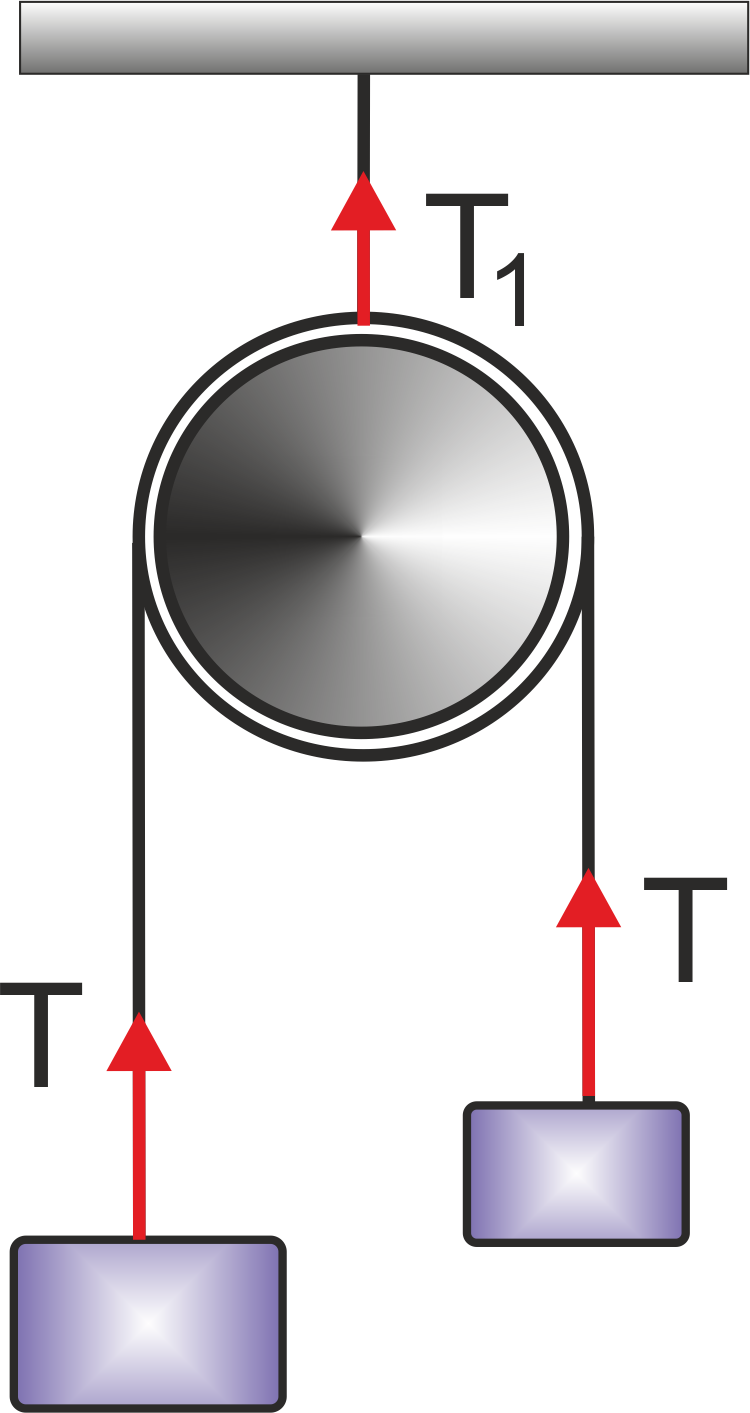
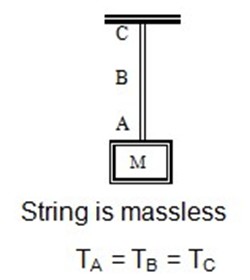
  • If a string a massless, the tension in it is same everywhere; on the other hand if a string is not massless (i.e. its mass is not negligible), tension at different points may be different.
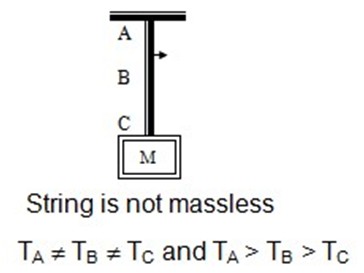
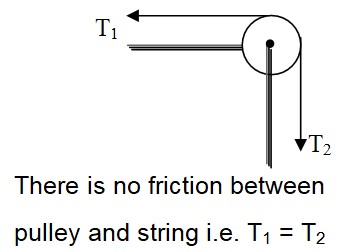
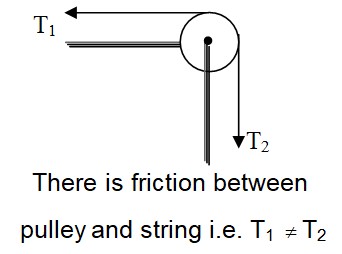
  • If friction is present between the pulley and the string, tension is different on the two sides of the pulley. But if the friction is absent between the pulley and the string, tension will be same on both sides of the pulley, provided the pulley is massless.

ELASTIC FORCE (Spring Force, FS )

An ideal spring follows Hooke’s law which says that “the force applied by a springs on bodies connected to it is proportional to its extension or compression (change in length from its natural length).”

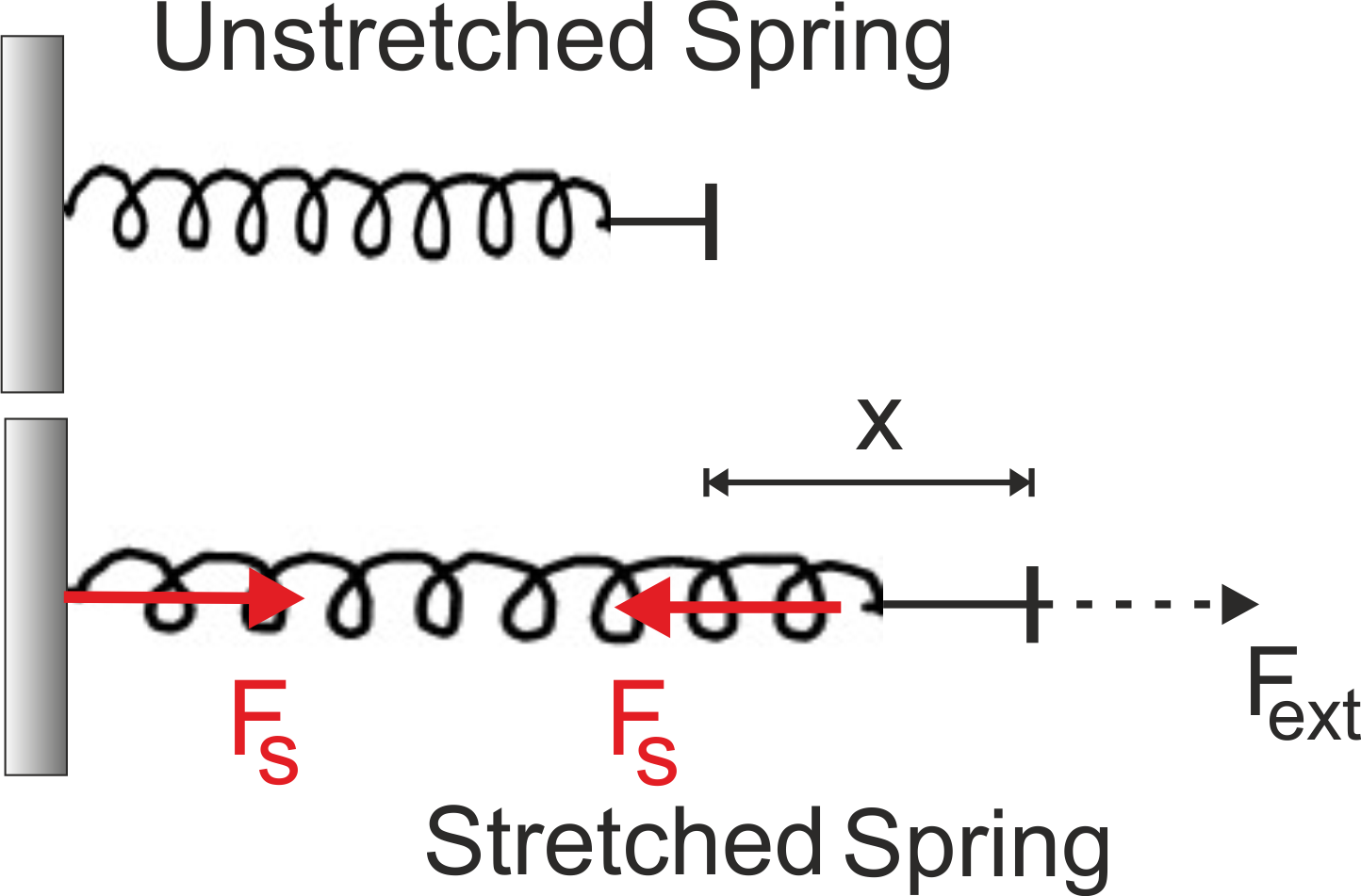
Consider a light spring which is connected to a vertical wall as shown in the figure. Suppose that it is pulled to the right by means of a force F, which cause the spring to get elongated by x over its over its natural length, then for instantaneous rest, spring force FS  will be equal to applied force and in opposite direction.

Then ,     FS ∝ – x

Or     FS = – k x             …………..[1]

where k is a constant, known as the spring constant. Its value depends upon characteristic of the spring.

Also In this case, the force applied by the spring on the wall is also equal to FS.

i.e The force exerted by a light spring on bodies connected to it at opposite ends are equal and opposite.

Forces commonly used in mechanics (Video)

In Hindi + English Mix

ARISTOTLE’S FALLACY

The Greek thinker, Aristotle (384 B.C– 322 B.C.), held the view that if a body is moving, something external is required to keep it moving.

Aristotelian law of motion may be phrased thus: An external force is required to keep a body in motion.

We will see later that Aristotelian law of motion is flawed. However, it is a natural view that anyone would hold from common experience. Even a small child playing with a simple (non-electric) toy-car on a floor knows intuitively that it needs to constantly drag the string attached to the toycar with some force to keep it going. If it releases the string, it comes to rest.

Then, what is the flaw in Aristotle’s argument? The answer is: a moving toy car comes to rest because the external force of friction on the car by the floor opposes its motion. To counter this force, the child has to apply an external force on the car in the direction of motion. When the car is in uniform motion, there is no net external force acting on it: the force by the child cancels the force (friction) by the floor.

The opposing forces such as friction (solids) and viscous forces (for fluids) are always present in the natural world. This explains why forces by external agencies are necessary to overcome the frictional forces to keep bodies in uniform motion.

So, Aristotle got the wrong conclusion because he failed to consider opposing forces like friction and viscous force.

FIRST LAW OF MOTION: (Newton’s First Law)

“A body cannot change its position of rest or of uniform motion in a straight line unless or until some unbalanced external force acts on it.”

Thus according to this law, if the total external force on a body is zero, then either

(a) Velocity = 0, i.e. body remains at rest. Or

(b)  Velocity = constant. This means

  1. The body can not change its speed.
  2. The body can not change its direction of motion.

This inability on the part of a body to change its state of rest or of uniform motion in a straight line by itself (without external force) is called inertia.

Thus, inertia is a fundamental property of matter.

Inertia of a body is measured by its mass. More the mass of the body more is its inertia.

NOTE:

  • Force is such a factor, which is essential for change in translational motion of a body.
  • The first law of motion defines the force.

THREE TYPES Of INERTIA:

Inertia of rest.

“It is the property of a body due to which, it cannot change its state of rest by itself (unless some unbalanced external force is applied on it)” . The following examples illustrate this property.

  1. When a horse suddenly starts galloping, the upper part of the rider’s body bends backwards. This is due to the reason that while the lower part of his body (in contact with the horse) moves forward, the upper part remains at rest due to inertia of rest.
  2. Due to the same reason, a person falls backwards when a train or a car etc. suddenly starts.
  3. When we beat a coat with a stick, the dust particles lying between the threads of the coat fall off. This is due to the reason that when the coat is suddenly set in motion. the dust particles tend to remain at rest due to the inertia of rest.
  4. If we jerk a piece of paper kept under a book quick enough, the book does not move. This is on account of the fact that the motion of the piece of paper is so quick that it is not imparted to the book. On account of inertia of rest, the book does not move.
  5. An apple falls down from the tree when its branch is shaken. This is due to the reason that when the tree-branch is shaken, it is set into motion whereas the apple tends to remain at rest due to inertia of rest. Due to this, the apple gets separated from the tree-branch and falls down due to gravity.
  6. A simple experiment that can be performed in the laboratory to demonstrate the inertia of rest, consists in placing a smooth ball coin on a smooth card resting on a hollow cup. When stick strikes the card, it flies off. But due to inertia of rest, the ball tends to continue in its state of rest and falls into the cup.
  7. Bodies of larger mass need larger initial effort for putting them into motion. It is on account of the fact that the bodies of large mass possess large inertia. Obviously, to put them into motion, large initial efforts are required.

Inertia of motion

                        It is the tendency of a body to remain in a state of uniform motion in a straight line.

“It is the property of a body due to which, it cannot change its speed by itself (unless some unbalanced external force is applied on it)”. Following are the examples.

  1. When we are travelling in a bus, we possess inertia of motion. When the bus suddenly stops, the upper parts of our bodies continue to be in motion. But our feet come to rest along with the bus and as such we fall forward.
  2. An athlete runs some distance before taking a jump. This is due to the reason that by running some distance before taking a jump, the athlete develops an inertia of motion. It is this inertia of motion which when added to the muscular effort, helps him to jump through a longer distance.
  3. If a person alights from a moving train without precaution, he is thrown forward due to the inertia of motion.
  4. When a horse at full gallop suddenly stops, the rider is thrown forward due to inertia of motion unless he is sitting on the horse very firmly.
  5. A ball thrown vertically upward by a person in a uniformly moving train comes back to his hand. This is due to the reason that the ball acquires the horizontal motion of the train and maintains it due to inertia of motion. Thus, if during the time the ball remains in air, the motion of the train and the position of the hands do not change, the ball comes back into the hands.
  6. It is due to the inertia of motion that a circus performer jumps up from the back of a running horse and after passing through a ring again comes back on the horse. Of course, during the time the performer is not on the horse, the direction and the speed of the horse should not change.
  7. When we shake off a drop of ink from a pen or shake a thermometer to make the mercury come down, we use the inertia of motion of ink drop in the pen or the mercury in the capillary tube of the thermometer.

Inertia of direction or directional inertia

                 “It is that property on account of which a body cannot change its direction of motion by itself (unless some unbalanced external force is applied on it)”. The following examples illustrate this property.

  1. When a vehicle is in motion, owing to the property of directional inertia, the mud sticking to its wheels flies off tangentially. In a vehicle, the mud-guards are so arranged that this flying mud, instead of spoiling the vehicle, sticks to them.
  2. It is due to the property of directional inertia that a stone which is being whirled in a circle flies off tangentially when the string suddenly snaps. It is the tension in the string which provides the necessary force (centripetal) to keep the stone in the circular path.
  3. When sharpening a knife, the sparks coming from the grindstone, fly off tangentially due to the property of directional inertia.

MOMENTUM

Momentum of a body is defined to be the product of its mass m and velocity v, and is denoted by p. Thus

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

p = m v         …………[2]       

Momentum is clearly a vector quantity and its direction is same as the direction of motion of the body (velocity vector).

Thus from equation [2] we conclude that

  • Momentum of a body is directly proportional to velocity of the body. i.e. for a given mass higher the velocity more is it momentum.
  • Momentum of a body is directly proportional to mass of the body. i.e. if two bodies of different mass are moving with same velocity, the heavier body is having the higher momentum.

NOTE: We can get number of examples where we find that ‘to change the momentum of a body some external force is needed on it’.

Newton’s Second Law

Newton's 2nd law_compressed

Newton’s Third Law

To every action, there is always an equal and opposite reaction. Newton’s law from an 1803 translation from Latin as Newton wrote

            “To every action there is always opposed an equal and opposite reaction”. 

Important points about the Third Law

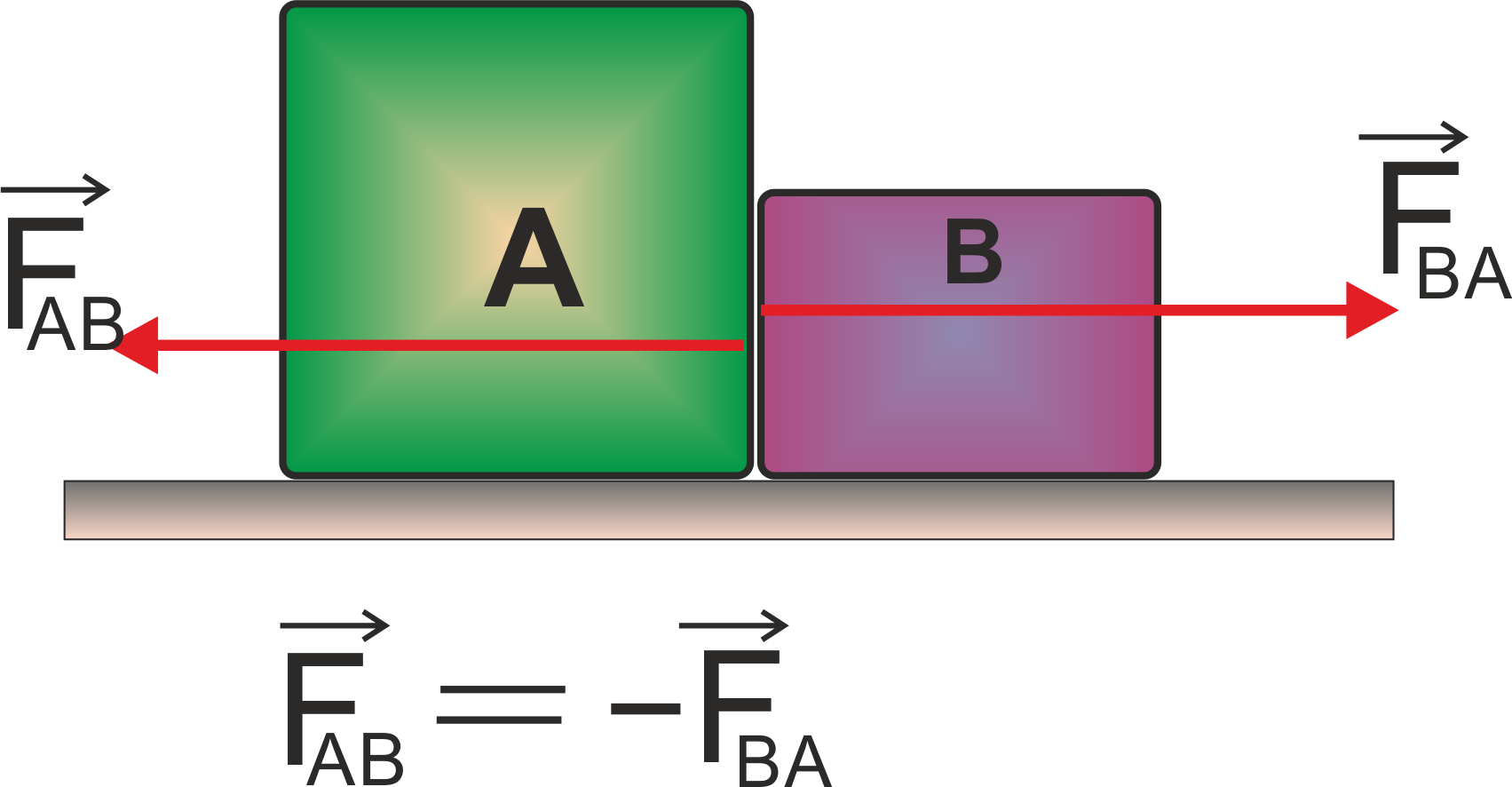
  • The terms ‘action’ and ‘reaction’ in the Third Law mean nothing else but ‘force’. Thus a simple conclusion from the Third Law is that “Forces always occur in pairs”.

If the force on a body A by B (FAB) is called ‘action’ then the force on B by A (FBA) can be called ‘reaction’, or vice-versa.

  • The terms ‘action’ and ‘reaction’ in the Third Law may give a wrong impression that action comes before reaction i.e. action is the cause and reaction the effect. There is no such cause-effect relation implied in the Third Law. The force FBA and the force FAB act at the same instant. Any one of them may be called action and the other as reaction. As these forces are equal and opposite, we may write

FBA = – FAB

  • Action and reaction forces act on different bodies and never act on the same body. Thus if we are considering the motion of any one body (A or B), only one of the two forces is relevant. It is an error to add up the two forces and claim that the net force is zero.

NOTE: However, if you are considering the system of two bodies as a whole, FAB  (force on A due to B) and FBA (force on B due to A) are internal forces of the system ( A + B). Then for the system, they add up to give a null force. (Since, FBA = – FAB , we get FBA + FAB = 0 )

Thus Internal forces in a body or a system of particles are canceled away in pairs. This is an important fact that enables the Second Law to be applicable to a body or a system of particles. [Principle of Conservation of Momentum]

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

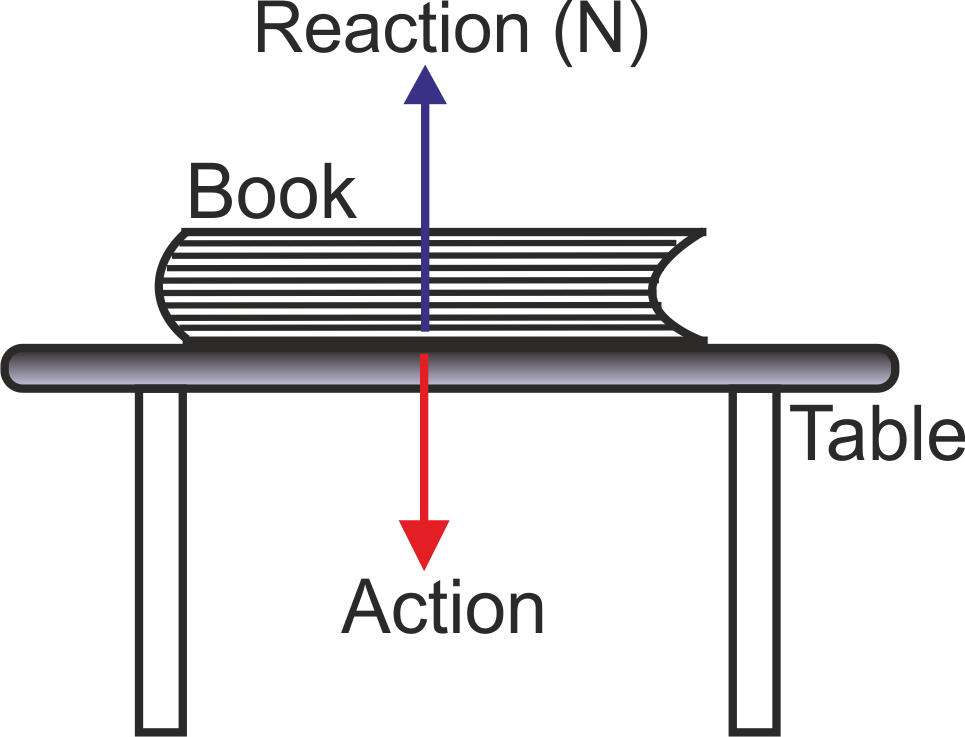
  1. Book kept on a table:

A book lying on a table exerts a force on the table which is equal to the weight of the book. This is the force of action. The table supports the book, by exerting an equal force on the book. This is the force of reaction, as shown in the figure. As the system is at rest, net force on it is zero. Therefore, forces of action and reaction must be equal and opposite.

  1. Walking: while walking a person presses the ground in the backward direction (action) by his feet. The ground pushes the person in forward direction with an equal force (reaction). The component of reaction in the horizontal direction makes the person move forward.
  1. Swimming: A swimmer pushes the water backwards (action). The water pushed the swimmer forward (reaction) with the same force. Hence the swimmer swims.
  1. Firing from a gun: When a gun is fired, the bullet moves forward (action). The gun recoils backwards (reaction).
  1. Flight of jet planes and rockets: The burnt fuel which appears in the form of hot and highly compressed gases escapes through the nozzle (action) in the backward direction. The escaping gases push the jet plane or rocket forward (reaction) with the same force Hence the jet or rocket moves.
  1. Rebounding of a rubber ball: When a rubber ball is struck against a wall or floor, it exerts a force on a wall (action). The ball rebounds with an equal force (reaction) exerted by the wall or floor on the ball.
  1. It is difficult to walk on sand or ice: This is because on pushing, sand gets displaced and reaction from sandy ground is very little. In case of ice, force of reaction is again small because friction between feet and ice is very small.
  1. Driving a nail into a wooden block without holding the block is difficult: This is because when the wooden block is not resting against a support, the block and nail both move forward on being hit with a hammer. However, when the block is held firmly against a support, and the nail is hit, an equal reaction of the support drives the nail into the block

Newton’s Laws Of Motion Video

In Hindi + English Mix

Horse and Cart Problem:

The various forces acting on a system of horse and cart at rest are shown in the figure. Here, the weight (mg) of the cart C is balanced by the Normal forces (N1 and N2) of the ground on the wheels.

The weight Mg of the horse H is balanced by the reaction R of the ground on the horse. The horse pulls the cart with a force T in the forward direction. The cart, in turn, pulls the horse with the same force T in the backward direction. These two forces are also balanced.

      While pulling the cart, the horse pushes the ground backwards with its foot by a force F (not shown in Fig) inclined at an angle q with the horizontal. As a reaction, the ground exerts force R on the horse equal and opposite to F.

      R can be resolved into two rectangular components:

      R sin θ vertically upwards, and R cos θ along the horizontal

            The component R cos θ tends to move the cart forward. This motion is opposed by the force of friction f between the cart and the ground. The cart will move only when R cos θ > f.

PROBLEM SOLVING STRATEGY Using NEWTON’S LAWS

Newton’s laws can be applied to study the motion of a body under the influence of a force or a set of forces. To make the study simpler, we take the each body (part of system) as separate identity. Then we show all the forces applied on the body (system) by surrounding bodies. The diagram showing all external forces acting on a body is called free body diagram. After representing the forces, the following steps may be adopted to study the motion of the body.

  1. Isolate the system and draw the forces acting on the system i.e. draw the free body diagram (F.B.D.).
  2. Consider the origin of the forces acting on each object. To do this find out the field forces acting on the object. Where ever contact is available show the contact forces carefully.
  3. With reference to direction of motion of the system, select suitable co-ordinate axes.
  4. Draw the forces in the given problem, decide whether the system at all can accelerate or not.
  5. If it accelerates, find its direction. Show the direction of acceleration with an arrow.
  6. In case of a composite problem of a number of bodies connected by strings and pulleys, find the relationship of accelerations of different bodies by constraint relationship [discussed later].
  7. Resolve all external forces along the chosen axes. Set up equation of motion along the individual axis as (Sext)x = x and (Sext)y = y. Finally, get the net acceleration as,
    = x + y, i.e. a = with direction w.r.t. x-axis as              θ = tan–1 (ay/ax).

Numerical Problems on Newton’s Laws

In Hindi + English Mix

MOTION IN A LIFT

Weight :  

The pull of earth on any body under its gravitational influence is called the weight of the body.   This force is directed towards the centre of the earth. This force produces an acceleration on the      body called the acceleration due to gravity.

       If, W m is the mass of body, then the actual (true) weight of the body is

        W= mg Newton, directed vertically downward.

Apparent Weight or Effective Weight of a body in a Lift:

The reading of a weighing machine or the force with which a body press the platform, on which it is kept, can be considered as the apparent weight or effective weight of the body.

When a man stands on a platform, it presses the platform with a force N downward. The force of same value is applied by the platform on the man in upward direction. This normal force is considered as the effective weigh or the apparent weight of the body.  

 If a body is on an accelerated platform, the apparent weight of the body becomes different than the actual weight (mg) of the body.

 Let a man of weight W = mg be standing in a lift. We consider the following cases.

Cases of Motion in a Lift-1
Cases of Motion in a Lift-2
 

Apparent Weight of a Body in a Lift

In Hindi + English Mix

Leave a Comment

************************************** Unique Offline ISC Classes (XI & XII) with Online Support

Get THREE days FREE Trial in 'ISC XI &XII Offline Classes' starting soon.

 

Join NOW !

No thanks, I’m not interested.

error: Content is protected !!