Contents
Light waves are transverse in nature; i.e., the electric field associated with a propagating light wave is always at right angles to the direction of propagation of the wave. [Remember there can be infinite number directions perpendicular to the direction of propagation]
Unpolarised light
A light beam in which the vibration of electric field vector take place randomly in every direction in a plane perpendicular to the direction of propagation of light, is known as unpolarised light.
So, in an unpolarised wave the displacement will be randomly changing with time though it will always be perpendicular to the direction of propagation.
Direction of propagation normal to plane of paper.
The direction of propagation is in the plane of paper.
We know light is emitted by atoms. The light pulse emitted by one atom in a single event has a fixed direction of electric field. However, the light emitted by different atoms, in general, has electric fields in different directions. Hence, the resultant electric field at a point keeps on changing its direction randomly and rapidly. Such a light is called unpolarised light.
The light emitted by an ordinary source such as electric lamp, a mercury lamp, a candle, the sun, are unpolarised light.
Plane Polarized light:
A light beam in which the vibration of electric field takes place in a plane perpendicular to the direction of propagation is known as plane polarized light.
In Fig Plane polarized light is shown as:
The direction of propagation is in the plane of paper
Direction of propagation normal to plane of paper.
Thus in a plane polarized light the electric field vectors of every light pulse lie in the same plane.
A plane polarized light can be generated by passing an unpolarised light through a polarizer (a polaroid, a Nicol prism or through some dichoric crystal, etc.)
Plane of vibration
An imaginary plane which contains the direction of propagation of the light beam & the direction of vibration of electric field vector is known as plane of vibration.
Plane of polarization
An imaginary plane, perpendicular to the plane of vibration and containing the direction of propagation of the plane polarized beam, is known as plane of polarization i.e., vibration of electric field vector takes place perpendicular to the plane of polarization.
NOTE: When unpolarised light is passed through a polarizer, the intensity of transmitted light is ideally half of the intensity of the incident light.
POLAROID
A polaroid consists of long chain molecules (quinine idosulphate) aligned in a particular direction. The electric vectors (associated with the propagating light wave) along the direction of the aligned molecules get absorbed. Thus, if an unpolarised light wave is incident on such a polaroid then the light wave will get linearly polarised with the electric vector oscillating along a direction perpendicular to the aligned molecules; this direction is known as the pass-axis (or transmission axis) of the polaroid.
- When unpolarised light passes through the polaroid, the transmitted light light becomes plane polarized with electric field vector (E – vector) parallel to the pass axis of the polaroid. [Intensity of the transmitted light becomes half of the intensity of the incident light]
Polaroids can be used to control the intensity, in sunglasses, windowpanes, etc. Polaroids are also used in photographic cameras and 3D movie cameras.
Law of Malus
“When a plane polarized light is incident on a polaroid, Intensity of emergent beam coming out of it is directly proportional to the square of cosine of angle between the direction of vibration of incident plane polarized light & axis of the polaroid (analyzer)”. i.e.,
I ∝ cos2θ
or,
I = I0 cos2θ
Where I0 is the intensity of the incident beam.
Proof of Law of Malus
Let the amplitude of electric field of the incident beam is E0, then the intensity of incident beam.
I0 = kE02 ……………..(1)
If the axis of Polaroid makes angle q with the direction of electric field, the amplitude of electric field vector that comes out the analyser is
E0’ = E0 cos θ
Intensity of emergent beam is I = kE02 or I = kE0’2 cos2θ
or,
I = I0 cos2θ ………..(2)
NOTE
- If a plane polarized light is incident on a polaroid with E – vector parallel to the pass axis, the light is completely transmitted through the polaroid.
- If a plane polarized light is incident on a polaroid with E – vector perpendicular to the pass axis, the light is completely transmitted through the polaroid.
- If a plane polarized light is incident on a polaroid with E – vector (E0) making an angle θ with the pass axis, the light is partially transmitted through the polaroid. (I µ cos2θ)
Polaroid as Analyzer
When a Polaroid is used to detect and study an incident light, it is called analyzer. To detect a plane polarized light the light is allowed to fall normally on the polaroid & then it is rotated slowly about an axis normal to its plane and at the same time intensity of the emergent beam is observed.
Case – 1: Plane Polarized Light
If the intensity of the emergent beam varies between 0 to a maximum, the incident beam is a plane polarized light. The vibration of plane polarized light along the optic axis of the polarized in the position when the intensity of the emergent beam is maximum.
Case – 2: Unpolarised Light
If the intensity of the emergent beam remains unchanged through out the whole rotation, the incident beam is unpolarised.
Case – 3: Partially Plane Polarized
The intensity of emergent beam various between maximum to a minimum but it never becomes zero.
Polarisation by Scattering
The light from a clear blue portion of the sky shows a rise and fall of intensity when viewed through a polaroid which is rotated. This is nothing but sunlight, which has changed its direction (having been scattered) on encountering the molecules of the earth’s atmosphere.
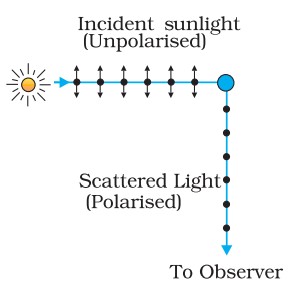
The incident sunlight is unpolarised. Under the influence of the electric field of the incident wave the electrons in the molecules acquire components of motion in both these directions. We have drawn an observer looking at 90° to the direction of the sun. Clearly, charges accelerating parallel to the double arrows do not radiate energy towards this observer since their acceleration has no transverse component. The radiation scattered by the molecule is therefore represented by dots. It is polarised perpendicular to the plane of the figure. This explains the polarisation of scattered light from the sky.
Polarisation by Reflection
(Brewster’s Law)
When unpolarised light is incident on the boundary between two transparent media, the reflected light is polarised with its electric vector perpendicular to the plane of incidence when the refracted and reflected rays make a right angle with each other.
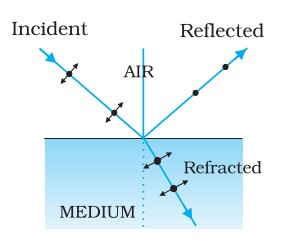
Thus when reflected wave is perpendicular to the refracted wave, the reflected wave is a totally polarised wave. The angle of incidence in this case is called Brewster’s angle and is denoted by iB. This angle also called polarising angle, iP.
Thus, for i = iB
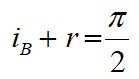
Or
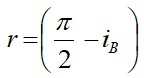
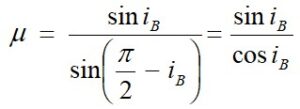
Or ![]()
- When unpolarised light is incident at on the surface of transparent medium at the Brewster angle, one of the two perpendicular components of the electric field is zero.
- At other angles (i.e. when angle of incidence other than polarizing angle or Brewster’s angle), the reflected light is partially polarised. When such light is viewed through a rotating analyser, one sees a maximum and a minimum of intensity but not complete darkness. In such light beam, although, both components are present but one component is stronger than the other.
- In partially polarized light, there is no stable phase relationship between the two perpendicular components since these are derived from two perpendicular components of an unpolarised
A SPECIAL CASE OF TOTAL TRANSMISSION
When an unpolarised beam of light is incident at the Brewster’s angle on an interface of two media, only part of light with electric field vector perpendicular to the plane of incidence will be reflected. Now by using a good polariser, if we completely remove all the light with its electric vector perpendicular to the plane of incidence and let this light be incident on the surface of the transparent surface (say, prism) at Brewster’s angle, we observe that for a this specific alignment of the polariser, the light incident on the transparent surface (prism) is completely transmitted and no light is reflected from the surface. We will then observe no reflection and there will be total transmission of light.
