Table of Contents
Wave Fronts and its Characteristics
Wave Front:
- A locus of points, which oscillate in phase is called a wavefront; thus a wavefront is defined as a surface of constant phase.
- The energy of the wave travels in a direction (i.e. direction of ray) is perpendicular to the wavefront.
Spherical Wave Front
- When a point source emits waves uniformly in all directions, then the locus of points which have the same amplitude and vibrate in the same phase are spheres and we get what is known as a spherical wave front.
Cylindrical Wave Front
- When a line source emits waves uniformly in all directions, then the locus of points which vibrate in the same phase are coaxial cylinders and we have what is known as a cylindrical wave front.
Plane Wave Front
- At a large distance from the source, a small portion of the sphere can be considered as a plane. So, a plane wave front is generated by a source at large distance.
HUYGENS PRINCIPLE
According to Huygens principle,
- Each point of the wavefront is the source of a secondary disturbance and the wavelets emanating from these points on the wavefront are usually referred to as secondary wavelets.
- The secondary wavelets emanating from these points spread out in all directions with the speed of the wave.
- If we draw a common tangent (ENVELOPE) to all these spheres, we obtain the new position of the wavefront at a later time.
Huygen’ Principle and Explanation of Refraction (Video)
Video Language: Hindi + English
Refraction of a Plane Wave
(When the ray moves from rarer medium to the denser medium)
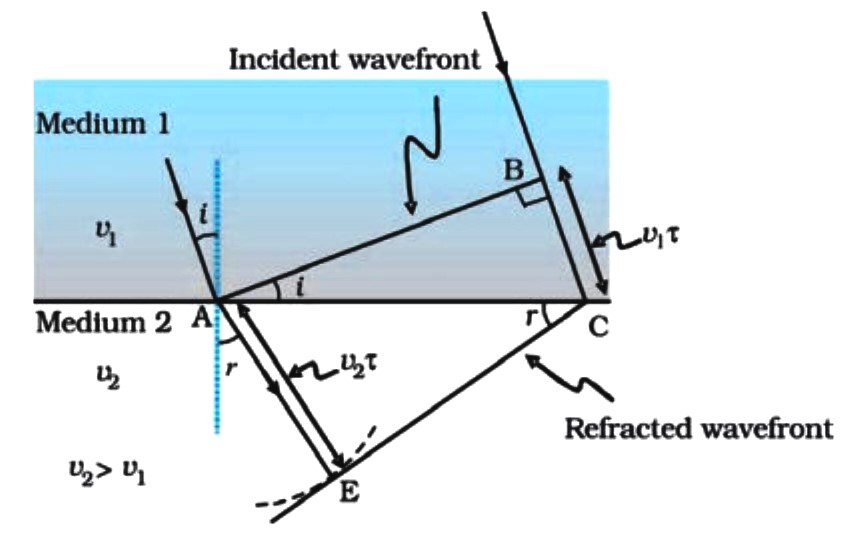
Let PP′ represent the surface separating medium 1 and medium 2, as shown in Fig.
Let v1 and v2 represent the speed of light in medium 1 and medium 2, respectively.
Let a plane wavefront AB propagating in the direction A′A incident on the interface at an angle i as shown in the figure.
Let τ be the time taken by the wavefront to travel the distance BC. Thus, BC = v1 τ.
In order to determine the shape of the refracted wavefront, let us consider an immaginary sphere of radius v2τ (the distance travelled by wave in medium 2 in time τ), with centre at the point A in the second medium. CE, which is a tangent plane drawn from the point C on to the sphere, represent the wavefront of the refracted wave.
If we now consider the triangles ABC and AEC, we get
………………………….(1)
and ………………………….(2)
Where, i and r are the angles of incidence and refraction, respectively.
Thus by Eq.(1)/Eq.(2), we get
………………….(3)
From the above equation, we get the important result that if r < i (i.e., if the ray bends toward the normal), the speed of the light wave in the second medium (v2) will be less than the speed of the light wave in the first medium (v1). This is the case when the first medium is rarer and second is denser.
Now, if c represents the speed of light in vacuum, then, the absolute refractive index of the 1st medium is
Or
…………….(4)
Similarly, the absolute refractive index of the 2nd medium is
Or
…………….(5)
Putting the values of v1 and v2 in equation
………………(6)
Or, it can be written as
m 1 sin i = m 2 sin r …………………….(7)
This is the Snell’s law of refraction.
NOTE: when a wave gets refracted into a denser medium (v1 > v2) the wavelength and the speed of propagation decrease but the frequency (= v/λ) remains the same.
Refraction at a Rarer medium
(When the ray moves from denser medium to a rarer medium)
We now consider refraction of a plane wave at a rarer medium, i.e., v2 > v1.
Proceeding in an exactly similar manner we can construct a refracted wave-front as shown in Fig.
The angle of refraction will now be greater than angle of incidence; however, we will still have m 1 sin i = m 2 sin r.
Since, in this case i < r, sin i < sin r. So, by above equation, m 1 > m 2
or m Denser > m Rarer .
CRITICAL ANGLE
“The angle of incidence in denser medium for which the angle of refraction is 90o, is called critical angle (ic)”.
Thus, if i = ic then r = 90° and sin r = 1. So, by equation (6) we get
………………..(8)
Obviously, for i > ic , there cannot be any refracted wave. For all angles of incidence greater than the critical angle, we will not have any refracted wave and the wave will undergo what is known as total internal reflection.
Reflection of a Plane Wave by a Plane Surface
Consider a plane wave with wavefront, AB, is incident at an angle i on a reflecting surface MN.
According to Huygen’s principle, points A and point B will act as secondary sources, from which secondary wavelets originate and propagate in every direction with speed of wave in the medium.
If v represents the speed of the wave in the medium and if τ represents the time taken by the wavelet to advance from the point B to C then the distance BC = vτ.
In order to construct the reflected wavefront we draw a sphere of radius vτ from the point A as shown in Fig. This sphere represents the wave front of secondary source A.
Let CE represent the tangent plane drawn from the point C to this sphere. Then CE will act as plane wavefront of the reflected wave. Obviously AE = BC = vτ.
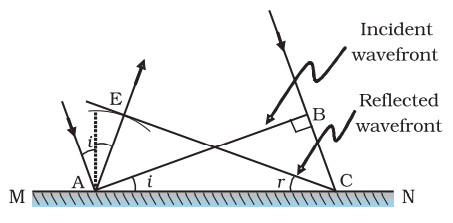
If we now consider the triangles EAC and BAC we will find that they are congruent [AE=BC= vτ , angle AEC = angle ABC = 90o,and AC is common]. Therefore, the angles i and r (as shown in Fig.) would be equal. This is the law of reflection.
Explanation of Reflection & Application of Huygen’s Principle(Video)
Video Language: Hindi + English
APPLICATIONS of HUYGENS PRINCIPLE
Once we have the laws of reflection and refraction, the behaviour of prisms, lenses, and mirrors can be understood. Here we just describe the behaviour of the wave-fronts as they undergo reflection or refraction.
In Fig. (a) We consider a plane wave passing through a thin prism. Clearly, since the speed of light waves is less in glass, the lower portion of the incoming wave-front (which travels through the greatest thickness of glass) will get delayed resulting in a tilt in the emerging wave-front as shown in the figure.
In Fig. (b) We consider a plane wave incident on a thin convex lens; the central part of the incident plane wave traverses the thickest portion of the lens and is delayed the most. The emerging wave-front has a depression at the centre and therefore the wave-front becomes spherical and converges to the point F which is known as the focus.
In Fig. (c) A plane wave is incident on a concave mirror and on reflection we have a spherical wave converging to the focal point F.
In a similar manner, we can understand refraction and reflection by concave lenses and convex mirrors.
Optical Path Length and Geometrical Path Length
From the above discussion it follows that the total time taken from a point on the object to the corresponding point on the image is the same measured along any ray.
Optical path length = refractive index X Geometrical path length
For example, when a convex lens focusses light to form a real image, although the ray going through the centre traverses a shorter path, but because of the slower speed in glass, the time taken is the same as for rays travelling near the edge of the lens.
