CBSE Syllabus
Composition and size of nucleus, nuclear force
Mass-energy relation, mass defect; binding energy per nucleon and its
variation with mass number; nuclear fission, nuclear fusion.
Contents
INTRODUCTION
- In every atom, the positive charge and mass are densely concentrated at the centre of the atom forming its nucleus.
- Experiments on scattering of α-particles demonstrated that the radius of a nucleus was smaller than the radius of an atom by a factor of about 104 . This means the volume of a nucleus is about 10–12 times the volume of the atom. In other words, an atom is almost empty.
- The nucleus contains most (more than 99.9%) of the mass of an atom.
ATOMIC MASSES AND COMPOSITION OF NUCLEUS
- Atomic mass unit (u), defined as 1/12th of the mass of the carbon (12C) atom.
- 1u = 1.660539×10-27 kg
- Accurate measurement of atomic masses is carried out with a mass spectrometer.
- Atoms of the same element, which exhibit the same chemical properties, but differ in mass, are called
- The nuclei of isotopes of a given element contain the same number of protons, but differ from each other in their number of neutrons.
- As the atoms of isotopes have identical electronic structure they have identical chemical behaviour and are placed in the same location in the periodic table.
- All nuclides with same mass number A are called isobars. For example, the nuclides 3 H1 and 3He2 are isobars.
- Nuclides with same neutron number N but different atomic number Z, for example 198Hg80 and 197 Au79 , are called
- It was found that practically every element consists of a mixture of several isotopes.
- The percentage of an isotope in the sample of an element is called its relative abundance. The relative abundance of different isotopes differs from element to element.
- The average mass of an atom of an element is obtained by the weighted average of the masses of all its isotopes.
- If w1, w2, w3 …….. are the relative abundance of isotope atoms of masses m1, m2, m3 ….. then the average mass of the atom of that element is
……….[1]
- The nucleus of the lightest atom of hydrogen, which has a relative abundance of 99.985%, is called the proton. The mass of a proton is
mp = 1.00727 u = 1.67262×10-27 kg
- The other two isotopes of hydrogen are called deuterium (2H1) and tritium (3H1). Tritium nuclei, being unstable, do not occur naturally and are produced artificially in laboratories.
- A proton carries one unit of fundamental charge and is stable.
- It was earlier thought that the nucleus may contain electrons, but this was ruled out later using arguments based on quantum theory.
- The number of electrons outside the nucleus of the atom is Z, the atomic number. The number of protons in the nucleus of the atom is, exactly Z, the atomic number. Thus the charge of the nucleus is (+Ze)
DISCOVERY OF NEUTRON
- In 1932 by James Chadwick who observed emission of neutral radiation when beryllium nuclei were bombarded with alpha-particles (α-particles are helium nuclei, to be discussed in a later section). It was found that this neutral radiation could knock out protons from light nuclei such as those of helium, carbon and nitrogen.
- Chadwick discovered that the neutral radiation consists of a new type of neutral particles called neutrons.
- From conservation of energy and momentum, Chadwick was able to determine the mass of new particle ‘as very nearly the same as mass of proton’.
- The mass of a neutron is now known to a high degree of accuracy. It is mn = 1.00866 u = 1.6749×10–27 kg
- A free neutron, unlike a free proton, is unstable. It decays into a proton, an electron and a antineutrino (another elementary particle), and has a mean life of about 1000s. It is, however, stable inside the nucleus.
- Z – atomic number = number of protons
N – neutron number = number of neutrons
A – mass number = Z + N = total number of protons and neutrons
- One also uses the term nucleon for a proton or a neutron. Thus the number of nucleons in an atom is its mass number A.
SIZE OF THE NUCLEUS
- By performing scattering experiments in which fast electrons, instead of α-particles (As in Rutherford’s, Geiger and Marsden experiment), are projectiles that bombard targets made up of various elements, the sizes of nuclei of various elements have been accurately measured.
- It has been found that a nucleus of mass number A has a radius
R = R0 A1/3 …………..[2]
Where R0 = 1.2 × 10–15 m = 1.2 fm; ( where 1 fm = 10–15 m).
- This means the volume of the nucleus, which is proportional to R3 is proportional to A.
- As the mass of a nucleus is approximately proportional to its atomic mass number, the density of nucleus is a constant, independent of A, for all nuclei.
- Different nuclei are like a drop of liquid of constant density. The density of nuclear matter is approximately 2.3 × 1017 kg m–3.
- This density is very large compared to ordinary matter, say water, which is 103 kg m–3. This is understandable, as nucleus is highly compressed material and most of the part of atom is empty.
MASS-ENERGY EQUIVALENCE
- Before the advent of this theory of special relativity (in Classical Physics) it was presumed that mass and energy were conserved separately in a reaction.
- Einstein showed in his theory of special relativity that mass is another form of energy and one can convert mass-energy into other forms of energy, say kinetic energy and vice-versa.
- Einstein gave the famous mass-energy equivalence relation
E = mc2 ……………………[3]
In this equation gives the value of energy that is equivalent to the m kg of mass.
c is the velocity of light in vacuum and is approximately equal to 3×108 m s–1.
The value of energy is in joule (J).
- Experimental verification of the Einstein’s mass-energy relation has been achieved in the study of nuclear reactions amongst nucleons, nuclei, electrons and other more recently discovered particles.
- So after the discovery of mass-energy equivalence the statement of conservation law is
“In a reaction the conservation law of energy states that the initial energy and the final energy are equal provided the energy associated with mass is also included”.
NUCLEAR BINDING ENERGY
- The nucleus is made up of neutrons and protons. Therefore it may be expected that the mass of the nucleus is equal to the total mass of its individual protons and neutrons taken togather. However, the actual mass of a nucleus (as measured by mass spectrometer), M is found to be always less than this.
- The difference in mass of all its constituents and actual mass of a nucleus, ∆M, is called the mass defect.
- Mass defect of a nucleus AXz is given by
∆M = [Z. mp + (A-Z) mn] − M ………….. [4]
- What is the meaning of the mass defect? It is here that Einstein’s equivalence of mass and energy plays a role. Since the actual mass of a AXz nucleus is less than that of the sum of the masses of its constituents {Z protons and (A-Z) neutrons, in the unbound state}, the equivalent energy of the AXz nucleus is less than that of the sum of the equivalent energies of its constituents.
- If one wants to break the AXz nucleus into Z protons and (A-Z) neutrons, this extra energy ∆M c2, has to be supplied. This energy is called Binding Energy of the nucleus.
- Thus energy required to break a nucleus into its constituent nucleons separated far away from one another is called Binding Energy of the nucleus.
- So Binding Energy (Eb) is related to the mass defect by equation
Eb = ∆ M c2
- The same amount of energy is lost during the formation of a Nucleus.
- In other words, If a certain number of neutrons and protons are brought together to form a nucleus of a certain charge and mass, an energy Eb will be released in the process. The energy Eb is called the binding energy of the nucleus.
- Binding energy per nucleon, Ebn, which is the ratio of the binding energy Eb of a nucleus to the number of the nucleons, A, in that nucleus. So
Ebn = Eb / A
- Physically binding energy per nucleon may be considered as the average energy per nucleon needed to separate a nucleus into its individual nucleons.
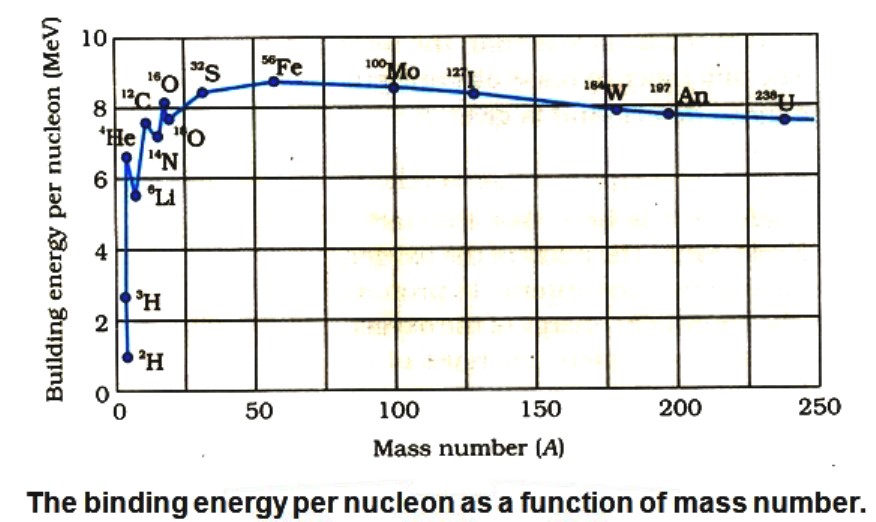
- We notice the following main features of the plot.
(i) the binding energy per nucleon, Ebn, is practically constant, i.e. practically independent of the atomic number for nuclei of middle mass number ( 30 < A < 170).
[The curve has a maximum of about 8.75 MeV for A = 56 and has a value of 7.6 MeV for A = 238].
(ii) Ebn is lower for both light nuclei (A < 170) and for heavy nuclei(A >170).
- We can draw some conclusions from these two observations:
(a) The force is attractive and sufficiently strong to produce a binding energy of a few MeV per nucleon.
(b) The constancy of the binding energy in the range 30 < A < 170 is a consequence of the fact that the nuclear force is short-ranged. The property that a given nucleon can influence only the nucleons close to it is also referred to as saturation property of the nuclear force.
(iii) A very heavy nucleus, say A = 240, has lower binding energy per nucleon compared to that of a nucleus with A = 120. Thus if a nucleus A = 240 breaks into two A = 120 nuclei, nucleons get more tightly bound. This implies energy would be released in the process. It has very important implications for energy production through fission.
(iv) Consider two very light nuclei (A ≤ 10) joining to form a heavier nucleus. The binding energy per nucleon of the fused heavier nuclei is more than the binding energy per nucleon of the lighter nuclei. This means that the final system is more tightly bound than the initial system. Again energy would be released in such a process of fusion. This is the energy source of sun and other stars.
NUCLEAR FORCE
To bind a nucleus together there must be strong attractive force acting between the nucleons, which is of a totally different kind of force. It must be strong enough to overcome the repulsion between the (positively charged) protons and to bind both protons and neutrons into the tiny nuclear volume.
Many features of the nuclear binding force are summarised below.
- (i) The nuclear force is much stronger than the Coulomb force acting between charges or the gravitational forces between masses.
[The nuclear binding force has to dominate over the Coulomb repulsive force between protons inside the nucleus.]
- (ii) The nuclear force between two nucleons falls rapidly to zero as their distance is more than a few femtometres (where 1 fm = 10–15 m). This leads to saturation of forces in a medium or a large-sized nucleus, which is the reason for the constancy of the binding energy per nucleon.
A rough plot of the potential energy between two nucleons as a function of distance is shown in the Fig. below.
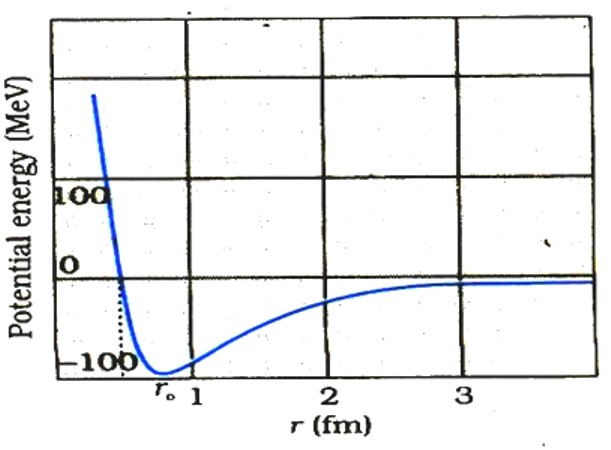
- The potential energy is a minimum at a distance r0 of about 0.8 fm.
- This means that the force is attractive for distances larger than 0.8 fm and repulsive if they are separated by distances less than 0.8 fm.
(iii) The nuclear force between neutron-neutron, proton-neutron and proton-proton is approximately the same. The nuclear force does not depend on the electric charge.
- Unlike Coulomb’s law or the Newton’s law of gravitation there is no simple mathematical form of the nuclear force.
NUCLEAR ENERGY
- The greater the binding energy, the less is the total mass of a bound system, such as a nucleus
- If nuclei with less total binding energy transform to nuclei with greater binding energy, there will be a net energy release.
- This is what happens when a heavy nucleus decays into two or more intermediate mass fragments (fission) or when light nuclei fuse into a heavier nucleus (fusion.)
FISSION
“The Process in which a heavy nucleus after capturing a slow neutron splits up into two lighter nuclei of comparable mass, is known as Fission” Thus a Neutron-induced nuclear reaction is fission.
The product nuclei are called ‘fission fragments’. In this process few fast neutrons and a huge amount of energy is released (in the form of K.E of fission fragments, KE of neutrons and -rays ).
92U235 + 0n1 92U236 56Ba141 + 36 Kr92 + 30n1 + Q
In general, the fission fragments are found to be the radioactive isotopes of elements of mass number 75 to 160. All fragment s undergo radioactive decay until fragments undergo radioactive decay until they reach some stable end product
The fragment products are radioactive nuclei; they emit β particles in succession to achieve stable end products. The energy released (the Q value ) in the fission reaction of nuclei like uranium is of the order of 200 MeV per nucleus.
- The disintegration energy in fission events first appears as the kinetic energy of the fragments and neutrons. Eventually it is transferred to the surrounding matter appearing as heat.
- The source of energy in nuclear reactors, which produce electricity, is nuclear fission.
- The enormous energy released in an atom bomb comes from uncontrolled nuclear fission.
Nuclear Chain Reaction
Under some favorable condition , the neutrons released from fission of U235 can be used to produce fission of three other U235 nuclei. This starts a chain reaction. This chain reaction continues until whole of the uranium is consumed .
In this process, no. of nuclei undergoing fission increases very fast , the process generates very large amount of energy per sec.
The no. of neutrons produced and available for further fission divided by the no. of neutrons present initially before the reaction is called reproduction factor or multiplication factor (K)*. This reproduction factor K should be at least equal to one so that nuclear fission may be sustained. If K > 1, rate of reaction increases fast and it tends towards the uncontrolled chain reaction. Unless the value of K is brought down very close to unity, the reactor will become supercritical and can even explode.
*Multiplication factor is a measure of growth rate of reaction.
Natural Uranium contains only 0.7% of U235, the remaining 99.3% being 92U238, which is not fissionable by thermal neutrons. Suppose we enrich the uranium, the enriched uranium which contains about 3% 92U235 , still a number of difficulties are faced.
- Neutron leakage : Some of the neutrons produced by fission leak out of the reactor and cease to be part of chain reaction. Leakage is a surface effect. Leakage can be reduced by making the reactor core large enough, thereby reducing the surface to volume ratio.
2.The Neutron Capture : The fast neutrons (2MeV) generated by the fission are slowed down in the moderate to thermal energies (V 0.04 eV) , they pass through a critical energy interval , between 1 to 100 eV, in which they are susceptible to non-fission capture by 92U238 nuclei. Such “resonance capture “ which results in the emission of γ-ray removes the neutrons from fission chain .
However, in nuclear reactions highly radioactive elements are continuously produced (radioactive waste).
Production of Plutonium (94Pu239) : The U238 nucleus , on capturing a neutron leads to the formation of plutonium. The reaction is
92U238 + 0n1 92U239 93Np239 + -1e0 + + Q
93Np239 94Pu239 + -1e0 +
Plutonium is highly radioactive and can also undergo fission under bombardment by slow neutrons.
Nuclear Reactor
A nuclear reactor is a device in which a self sustained controlled chain reaction is produced in a fissionable material.
Important parts:
- Fuel: The fissionable material 92U235 or Plutonium 94Pu239 is used as fuel. Uranium fuel is in the form of uranium oxide pellets, which are inserted end to end into long hollow metal tubes constituting the fuel rods.
- Modorator : It is used to slow down the fast neutrons coming out of a fission to the thermal energies (0.04eV).
A good moderator has two properties (1) it slows down the neutrons by elastic collisions (2) it does not remove the neutrons by absorbing them .The commonly used moderators are heavy water and graphite.[ Chadwick’s experiments demonstrated that in an elastic collision with hydrogen , the neutrons almost come to the rest and the proton carries away its energy. So, light nuclei work as most effective moderators.]
Heavy water (D2O) is used in reactors using natural uranium as fuel. This is because it has lesser absorption probability of neutrons than ordinary water.
The liquid moderator surrounds the bundle of fuel rods and thus forms the core of the reactor. [This geometric arrangement increases the probability that the on1 produced in the fuel rod, will find itself in the moderator when it passes through the critical energy interval (1 eV to 100 eV). Once the neutron has reached to thermal energy, it hits the fuel rod and produce the fission event]
- Control rods : These are the cadmium or boron rods which control the reaction rate in a reactor . These rods absorb the on1 readily and are inserted into the core to reduce the reaction rate and to reduce the operating power level. When the rods are with drawn, it increases the power level.
- Safety Rods : In case of emergency a special set of control rods, known as ‘shut off rods’ can be inserted into the reactor . This immediately absorb the neutrons and the chain reaction stops.
- Coolant : The energy released inside the reactor in the form of heat is removed by the coolant . For this purpose water, heavy water and CO2 is flown in the reactor.
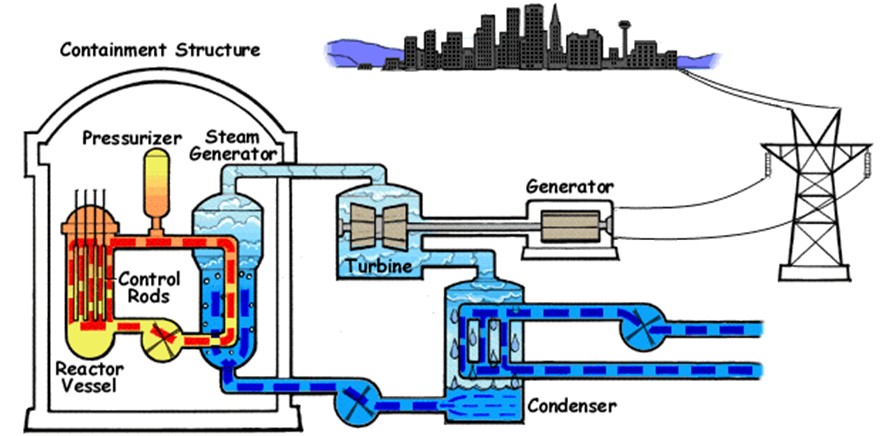
The fig. shows the pressurized water reactor. In such a reactor heavy water is used as moderator as well as coolant. In the ‘primary-loop’ water is circulated through the reactor vessel and transfers energy at high temperature and pressure (about 600 K and 150 atm) to the steam generator, which is part of secondary loop. In the steam generator, evaporation provides high-pressure steam to operate the turbine that divides the electric generator. The low pressure steam form the turbine is cooled and condensed to water and forced back into the steam generator.
NUCLEAR FUSION
When two light nuclei fuse to form a larger nucleus, energy is released,
because the larger nucleus is more tightly bound, and having higher value of binding energy per nucleon.
Some examples of such energy liberating nuclear
fusion reactions are :
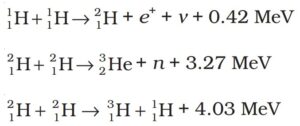
For fusion to take place, the two nuclei must come close enough so that
attractive short-range nuclear force is able to affect them. However,
since they are both positively charged particles, they experience coulomb
repulsion. They, therefore, must have enough energy to overcome this
coulomb barrier. The height of the barrier depends on the charges and
radii of the two interacting nuclei.
We can estimate the temperature at which two
protons in a proton gas would (averagely) have enough energy to
overcome the coulomb barrier:
(3/2)k T = K ≈ 400 keV, which gives T ~ 3 × 109K.
When fusion is achieved by raising the temperature of the system so
that particles have enough kinetic energy to overcome the coulomb
repulsive behaviour, it is called thermonuclear fusion.
